V.generalize tutorial
MODULE
- GRASS 7.x v.generalize
TUTORIAL
Introduction
This tutorial presents and explains the functionality of GRASS vector module v.generalize. This module implements generalization operators for GRASS vector maps. The topics covered in this tutorial are: simplification, smoothing, network generalization and displacement. For the basic introduction to these operators check the v.generalize man page, or for the exhausting introduction check McMaster and Shea (TODO: add reference).
It is recommended to read the official man page before reading this document, or read these two documents at the same time since this tutorial does not contain the (detail) descriptions of input parameters whereas the man page has very few examples and no pictures at all. (Even the author of module and both of the documents must have consult the man page several times....) This document is also meant to be a "report" showing the work done during the Google Summer of Code 2007.
Most of the examples in this text work with Spearfish dataset, which can
be downloaded here. Also, this
tutorial assumes that the user is already running GRASS session with the Spearfish
location and a monitor opened. Also, if you click on any picture here, it will be shown in its full size.
All the algorithms presented in this document (try to) preserve the topology of the input maps. This means, for example, that the smoothing and simplification methods never remove the first and last points of lines and that displacement preserves the junctions.
Simplification
v.generalize implements many simplification algorithms. The most widely used is Douglas-Peucker algorithm (TODO: reference). We can apply this algorithm to any vector map in the following way:
v.generalize input=roads output=roads_douglas method=douglas threshold=50
The explanation of the line above is following: Run v.generalize, apply Douglas-Peucker algorithm with threshold equals to 50 to the map roads and store the output in vector map output_douglas. The last output line produced by this module:
Number of vertices was reduced from 5468 to 2107[38%]
means that the input file (roads) has 5468 vertices in total and the new map (roads_douglas) has only 2107 vertices which is only 38% of original. On the other hand, if we run the commands:
d.vect roads d.vect roads_douglas col=blue
We can see that there are no significant differences between the input and output maps. "Only the details were removed".
The amount of the details removed can be specified by parameter: threshold. It is the case that the output map has fewer vertices and details for greater values of threshold. For example, if we run
v.generalize input=roads output=roads_douglas method=douglas threshold=200 --overwrite
we obtain a map with only 1726 vertices. A disadvantage of the command above is that
it never removes the lines. If we also want to remove the small lines, we need to run
the command above with the -r flag. If the -r flag is presented, lines shorter than
threshold and areas with areas less than threshold are removed:
v.generalize -r input=roads output=roads_douglas method=douglas threshold=200 --overwrite
Fixme: -r flag and method=remove_small have been removed. Try v.clean for removing small areas or v.edit map=mapname type=line tool=delete query=length thresh=0,0,-0.5
In this case, roads_douglas has only 850 vertices and it contains 387 lines whereas
the original map (roads) contains 825 lines. In this case, the output map has very few details,
but the basic shapes and topology are preserved:
It is also possible remove small lines/areas only (without any simplification). This is achieved
by method=remove_small:
v.generalize input=roads output=roads_remove_small method=remove_small threshold=200
produces following map with 399 lines. (Note removed lines in the upper left corner)
Douglas-Peucker Algorithm has very reasonable results, but it is very hard to find(guess) the right value of threshold. Moreover, it is also impossible to simplify each line to (for example) 40%. Exactly for such cases, v.generalize provides method=douglas_reduction. This algorithm is a modification of Douglas-Peucker Algorithm which takes another paratemer reduction which denotes (approximate) simplification of lines. For example,
v.generalize input=roads output=roads_douglas_reduction method=douglas_reduction \ threshold=0 reduction=50 --overwrite d.erase d.vect roads_douglas_reduction
produces following map with 3018 vertices (55%). (Note that there are almost no differencies between the original and the new map)
Also observe that the following commands are equivalent
v.generalize input=in output=out method=douglas threshold=eps v.generalize input=in output=out method=douglas_reduction threshold=eps reduction=100
Another algorithm implemented in this modules is "Vertex Reduction". This algorithm removes the consecutive poins (on the same line) which are closer to each other than threshold. For example,
v.generalize input=in output=out method=reduction threshold=0
removes duplicate points. More precisely, if two consecutive points have the same coordinates then the second point is removed and the first is preserved. The last two algorithm implemented by this module are "Lang" and "Reumann-Witkam" algorithm. For more information about these two algorithms, please see the v.generalize man page.
Results
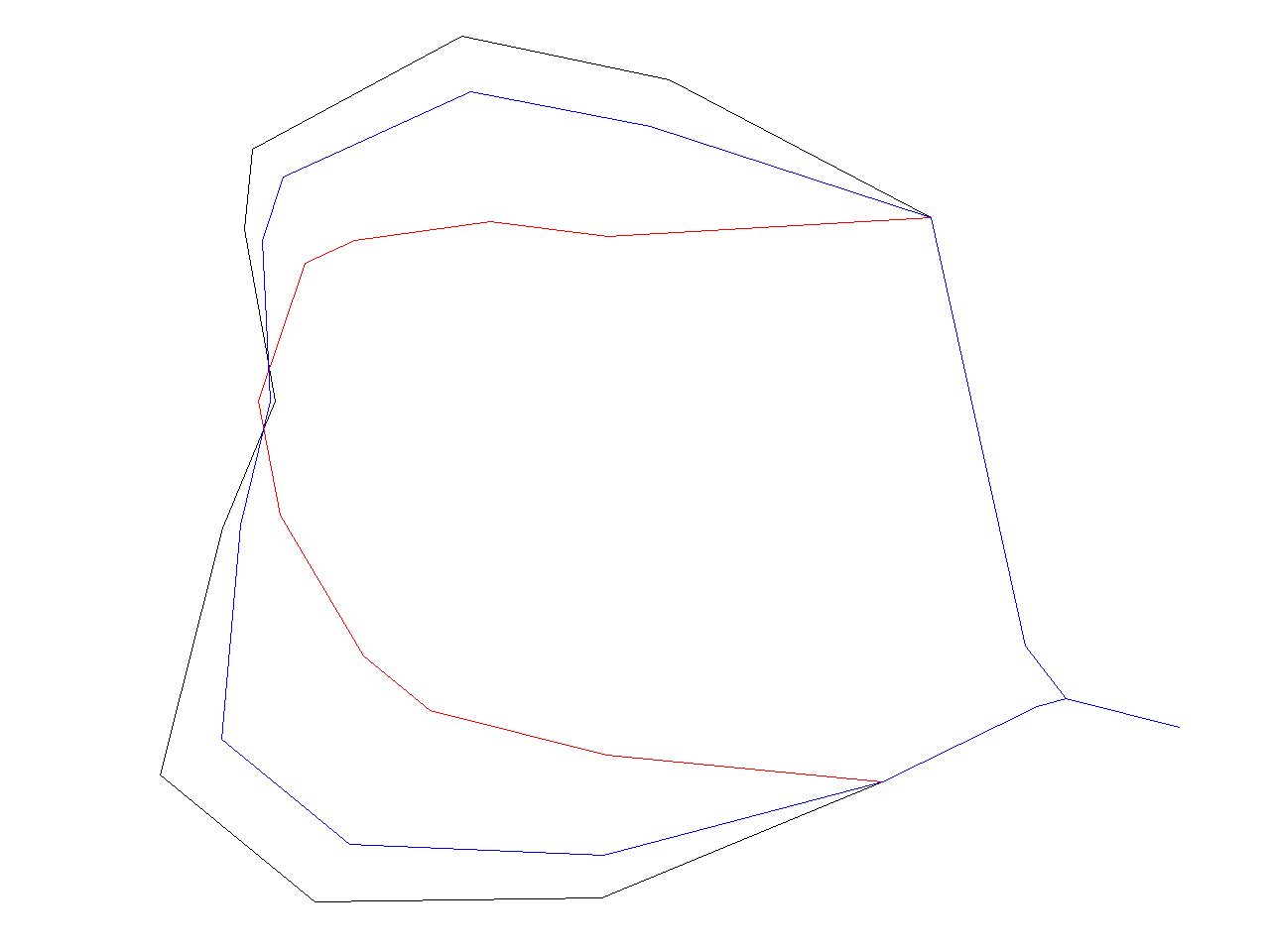
The following four pictures show the results obtained by Reumann, Douglas, Lang and Vertex Reduction algorithm resp. The algorithms were run with threshold set to 50 and Lang algorithm with look_ahead=7.
- Simplification algorithms
-
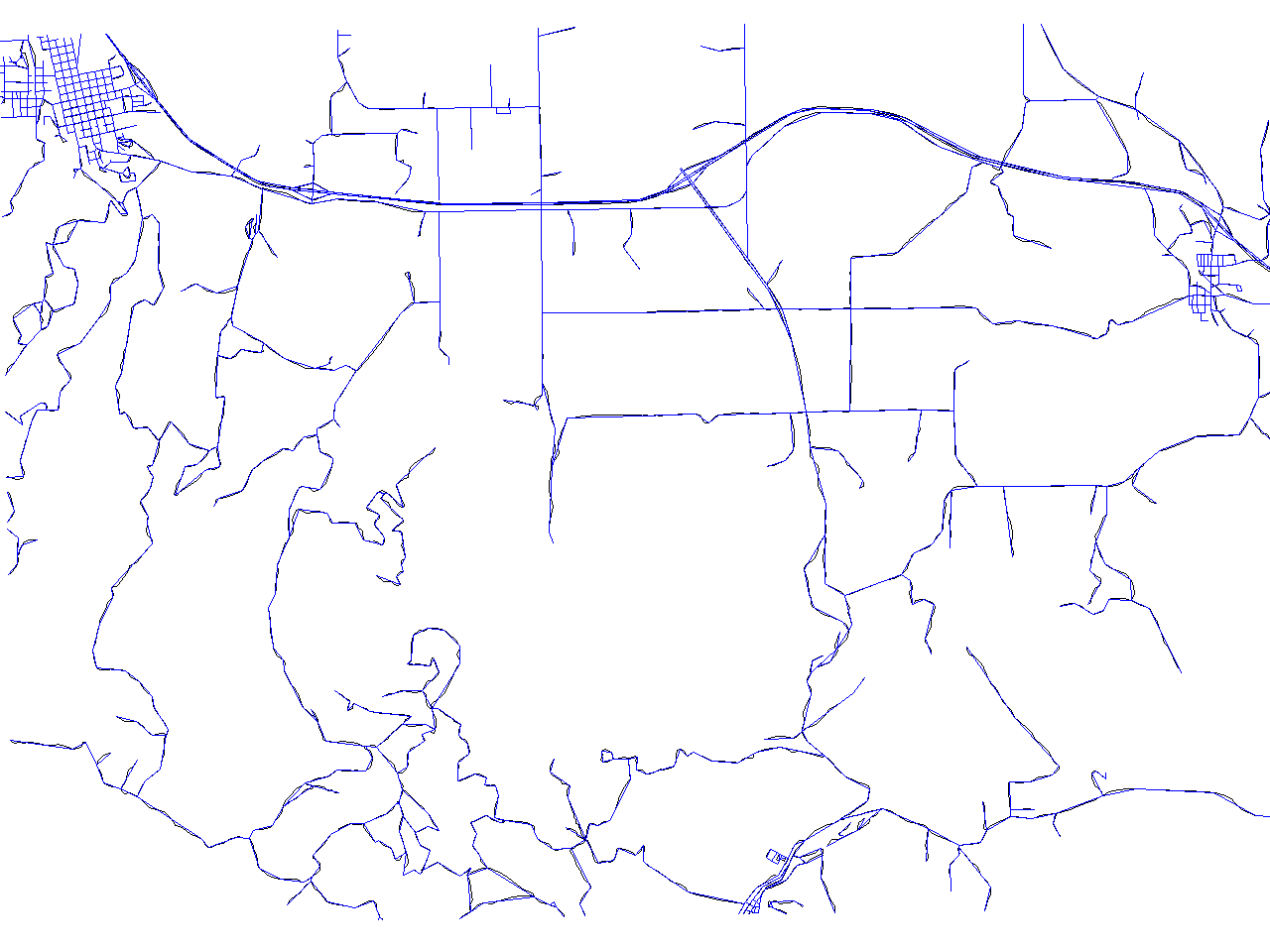
Reumann-Witkam algorithm result containing 2522 [46%] points
-
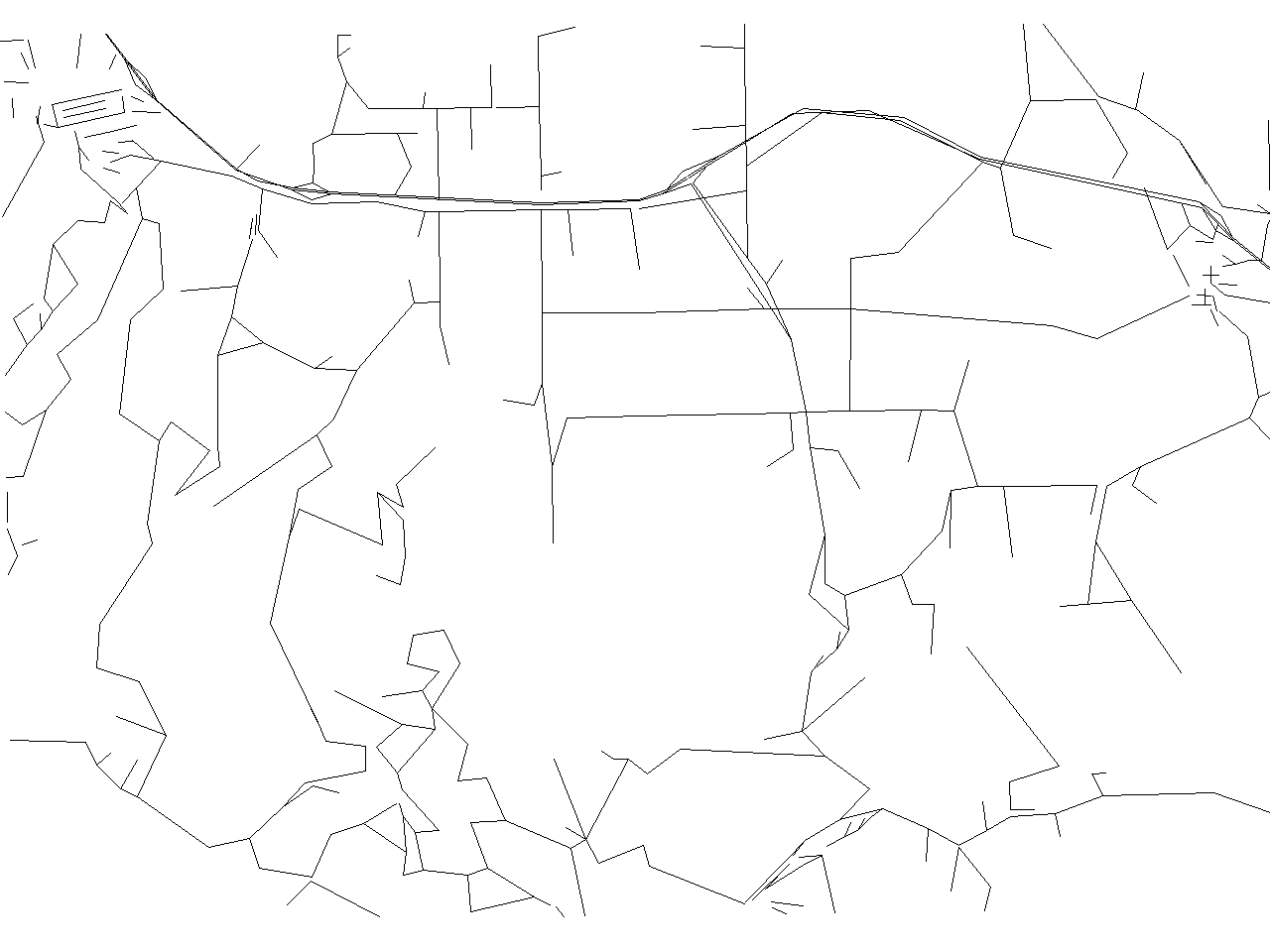
Douglas algorithm result containing 2107 [38%] points
-
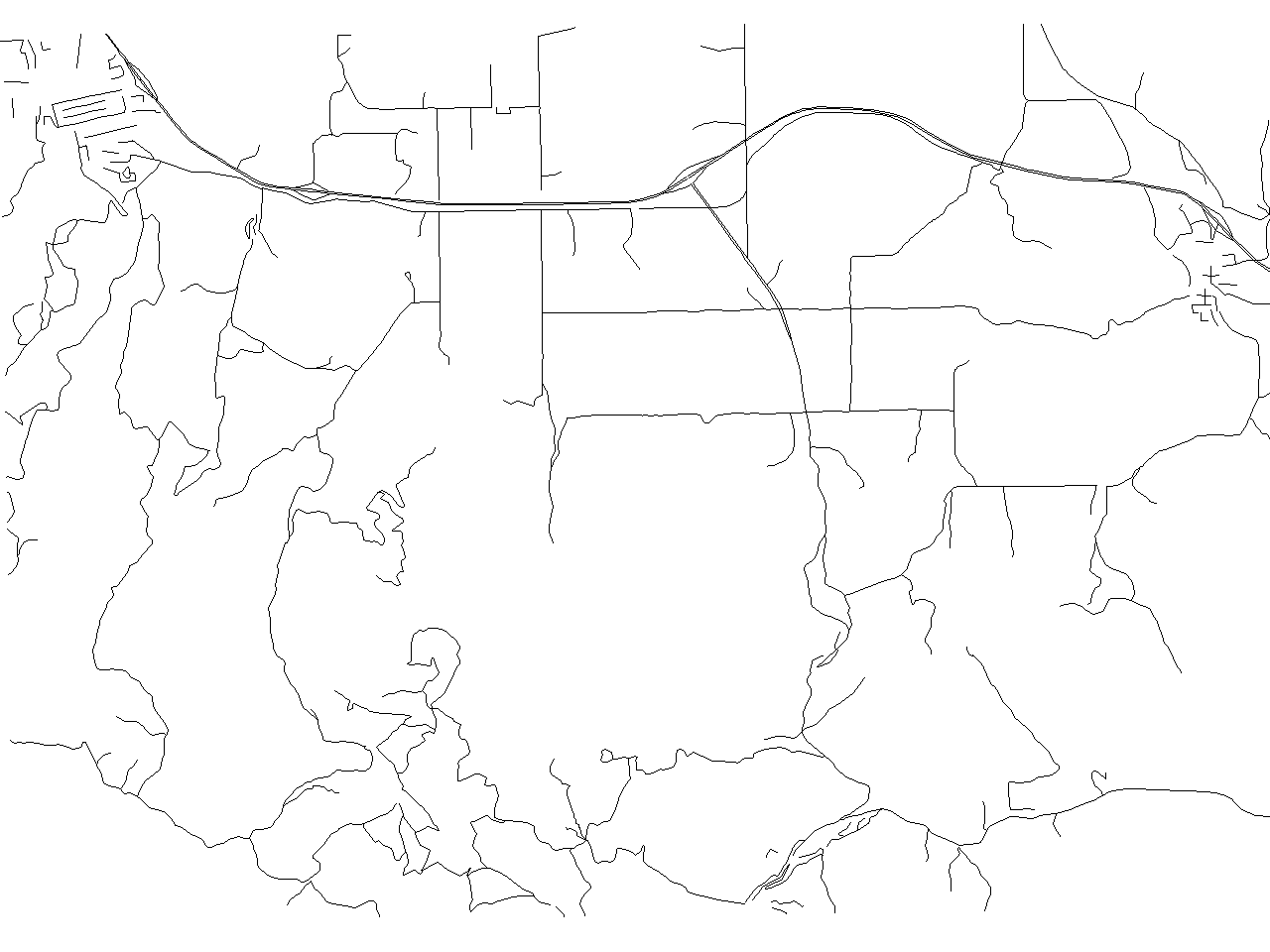
Lang algorithm result containing 2160 [39%] points
-
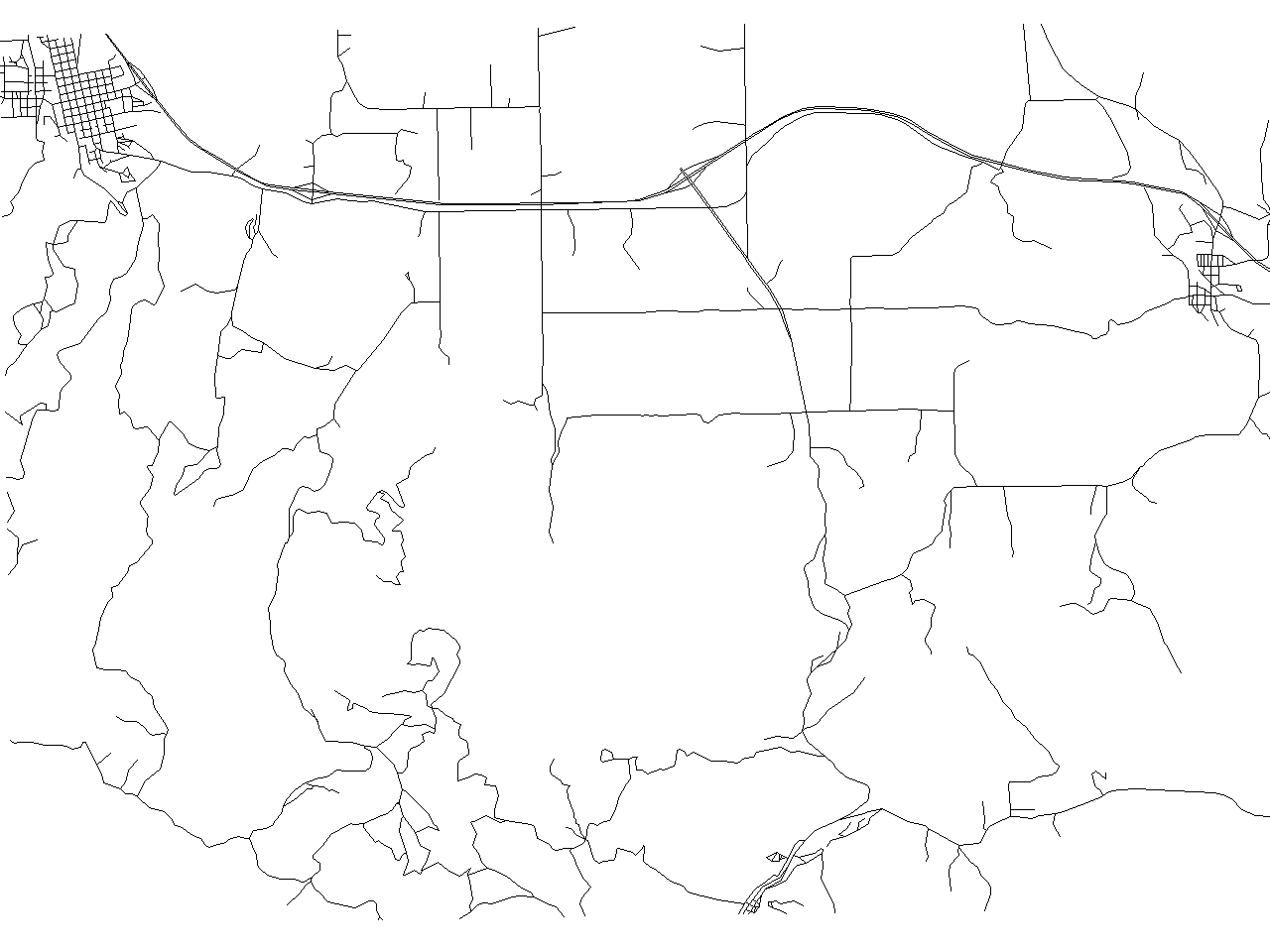
Vertex Reduction algorithm result containing 4296 [78%] points
The map produced by
- Reumann-Witkam algorithm contains 2522 [46%] points,
- Douglas: 2107 [38%] points,
- Lang: 2160 [39%] and
- Vertex Reduction: 4296 [78%].
Smoothing
v.generalize also supports many smoothing algorithm. For basic descriptions, please consult the v.generalize man page.
Probably, the best results are produced by "Chaiken", "Hermite" and "Snakes" algorithms/methods. However, the remaining algorithms may also produce very reasonable results. Although the Chaiken and Hermite methods may produce the maps with a lot of new points, the methods presented above (simplification) provide a good tool for tackling this problem.
If we run the following command
v.generalize input=roads output=roads_chaiken method=chaiken threshold=1
we get a new map with 33364[640%] vertices.
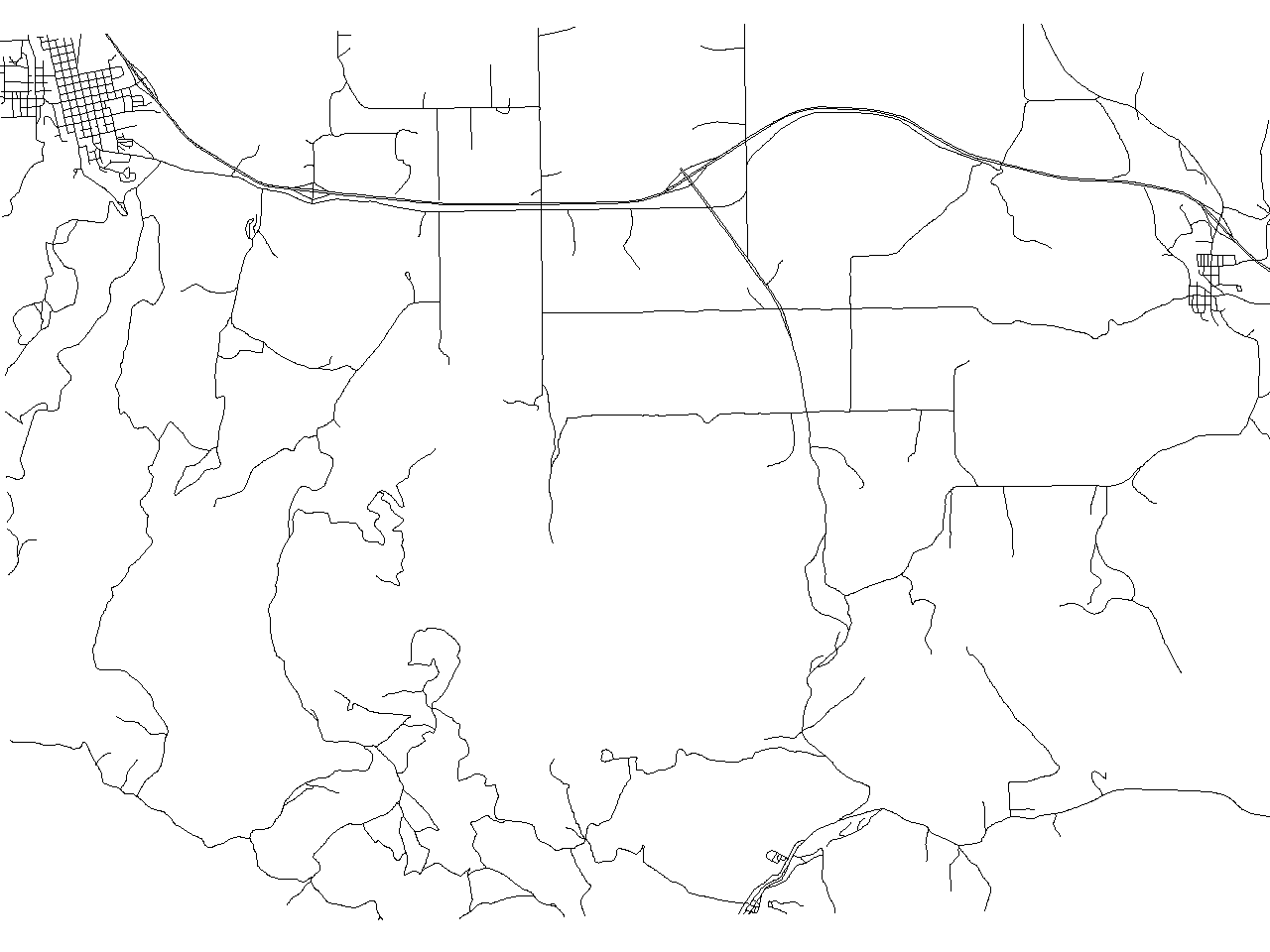
This map looks almost exactly the same as the original map at the current level of detail as the picture below shows. This pictures was produced by the command:
d.erase d.vect roads d.vect roads_chaiken col=blue
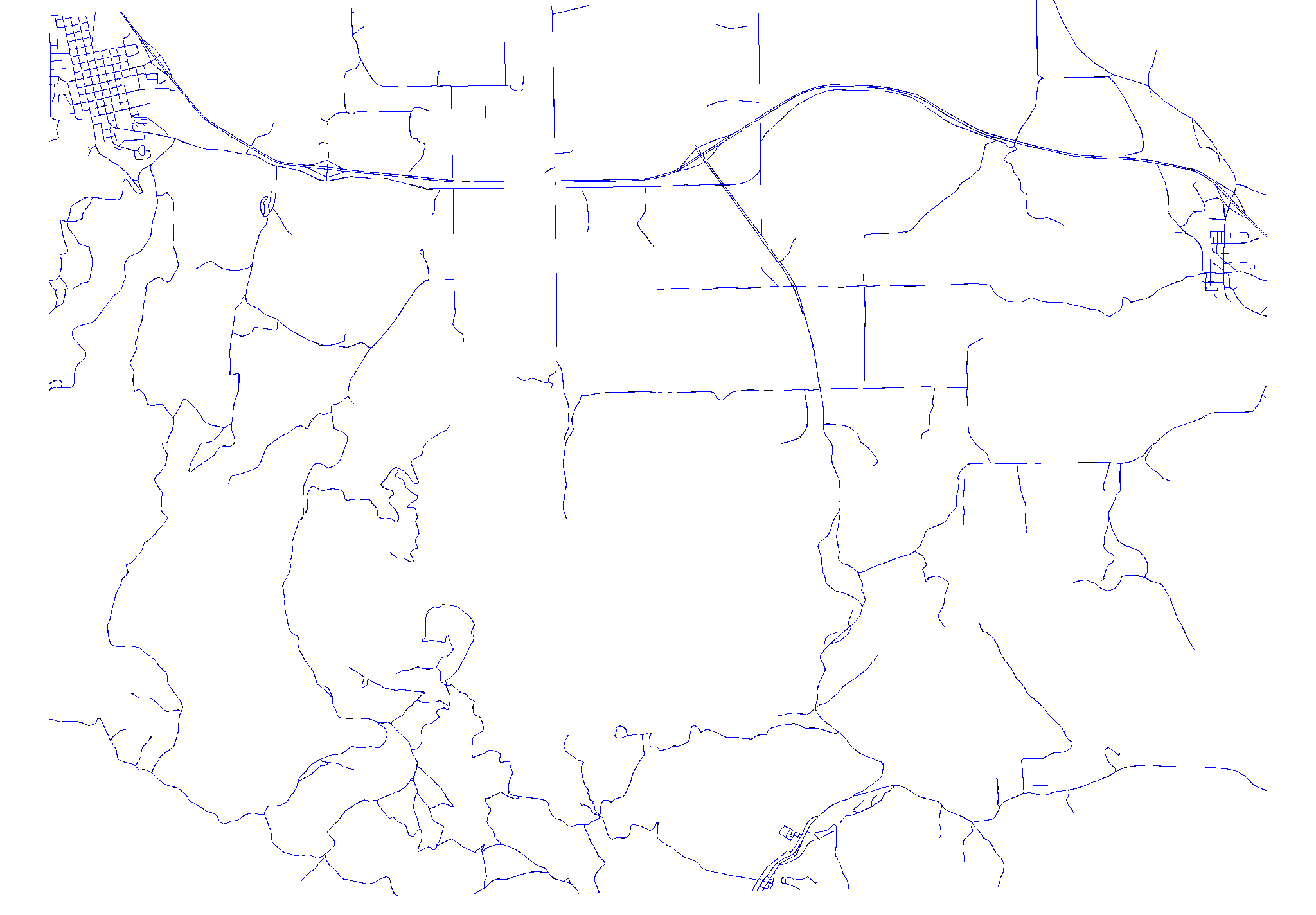
However, if we zoom to a small region, we can see that the new map consists of smooth(er) lines which (very reasonable) approximate the original ones.

If we apply "Hermite" method instead, we will obtain a map with 14640[267%] vertices.
v.generalize input=roads output=roads_hermite method=hermite threshold=1

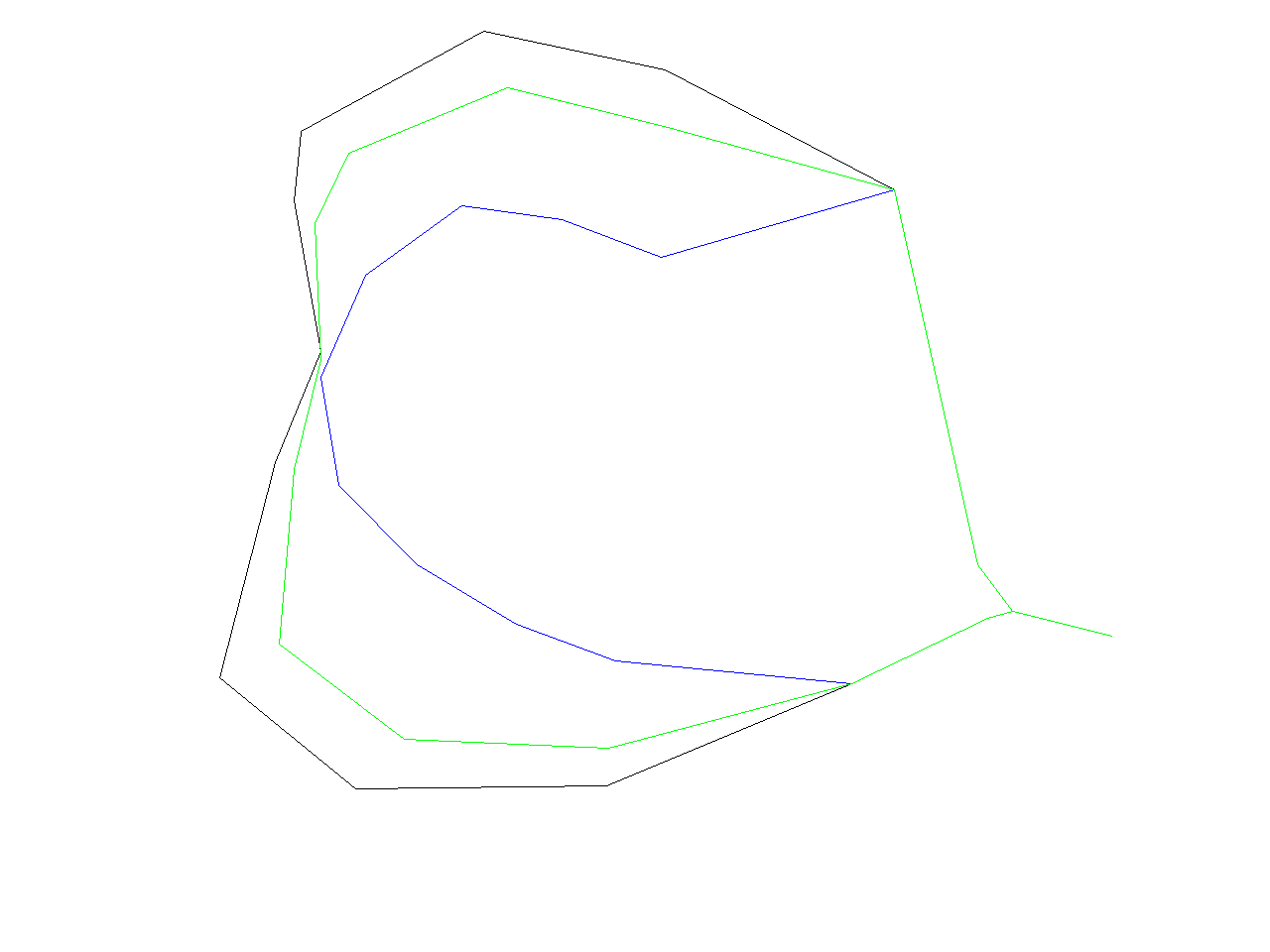
Note, that a difference between "Chaiken" and "Hermite" is that the lines produced by "Chaiken" "inscribe" the original lines whereas the "Hermite" lines "circumscribe" the original lines as can be seen in the picture below. (Black line is original line, green line is "Chaiken" and blue is "Hermite")

The algorithms mentioned above are suitable for smooth approximation of given lines. On the other hand, if the aim of smoothing is to "straighten" the lines then the better results are achieved by the other methods. For example,
v.generalize input=roads output=roads_sa method=sliding_averaging look_ahead=7 slide=1
At first sight, we can see that roads_sa contains smooth and straight lines which
preserve the original shape of the lines. This difference is obvious if we zoom to a small
region of a map (see below. Again, original line is black, new line is blue)
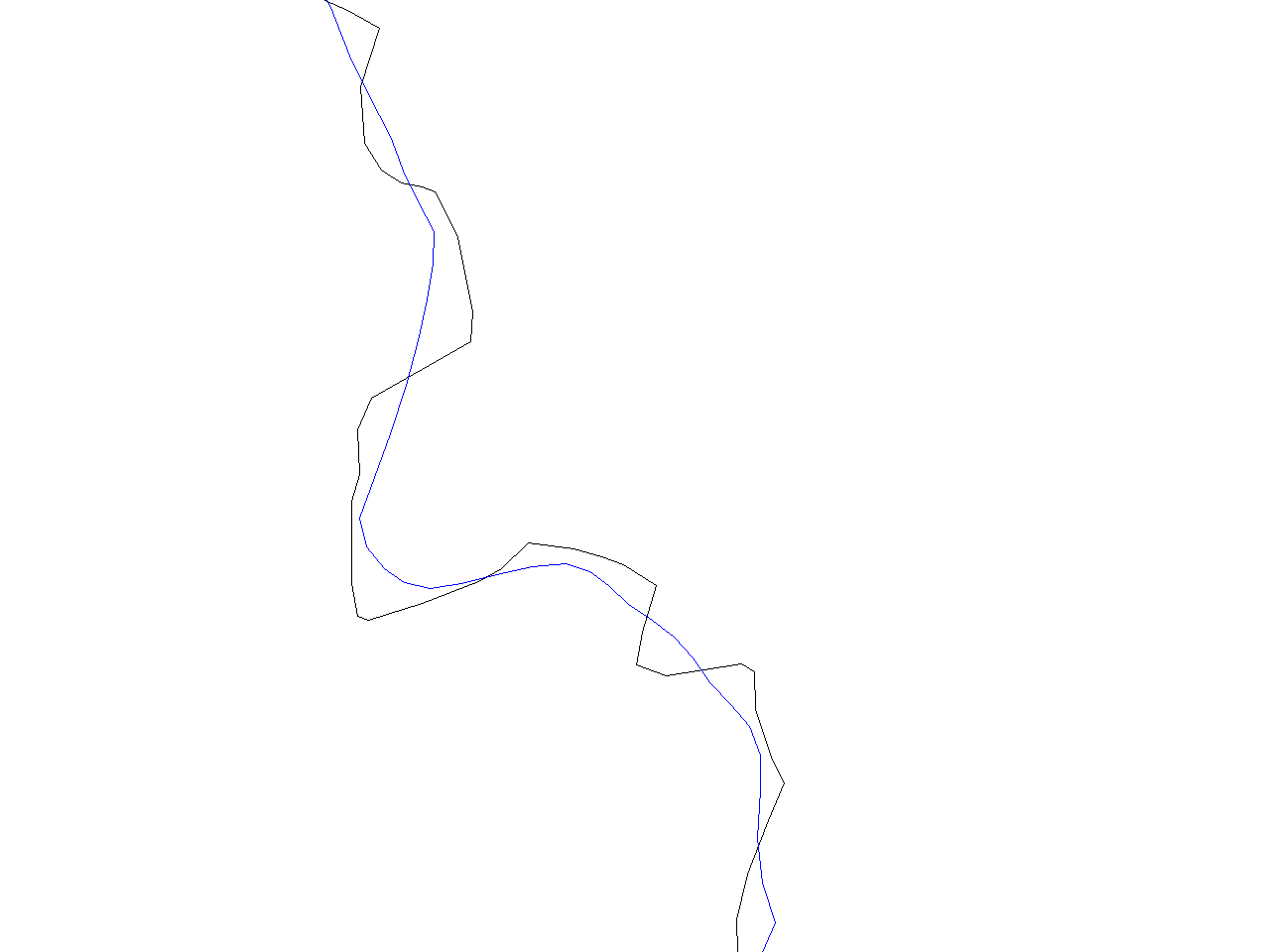
If the lines are "too straight" then we can set "slide" to a smaller value to obtain the lines which better preserve the original shape. In the picture below, original line is black, line produced by "slide=1" is blue and "slide=0.3" is green.
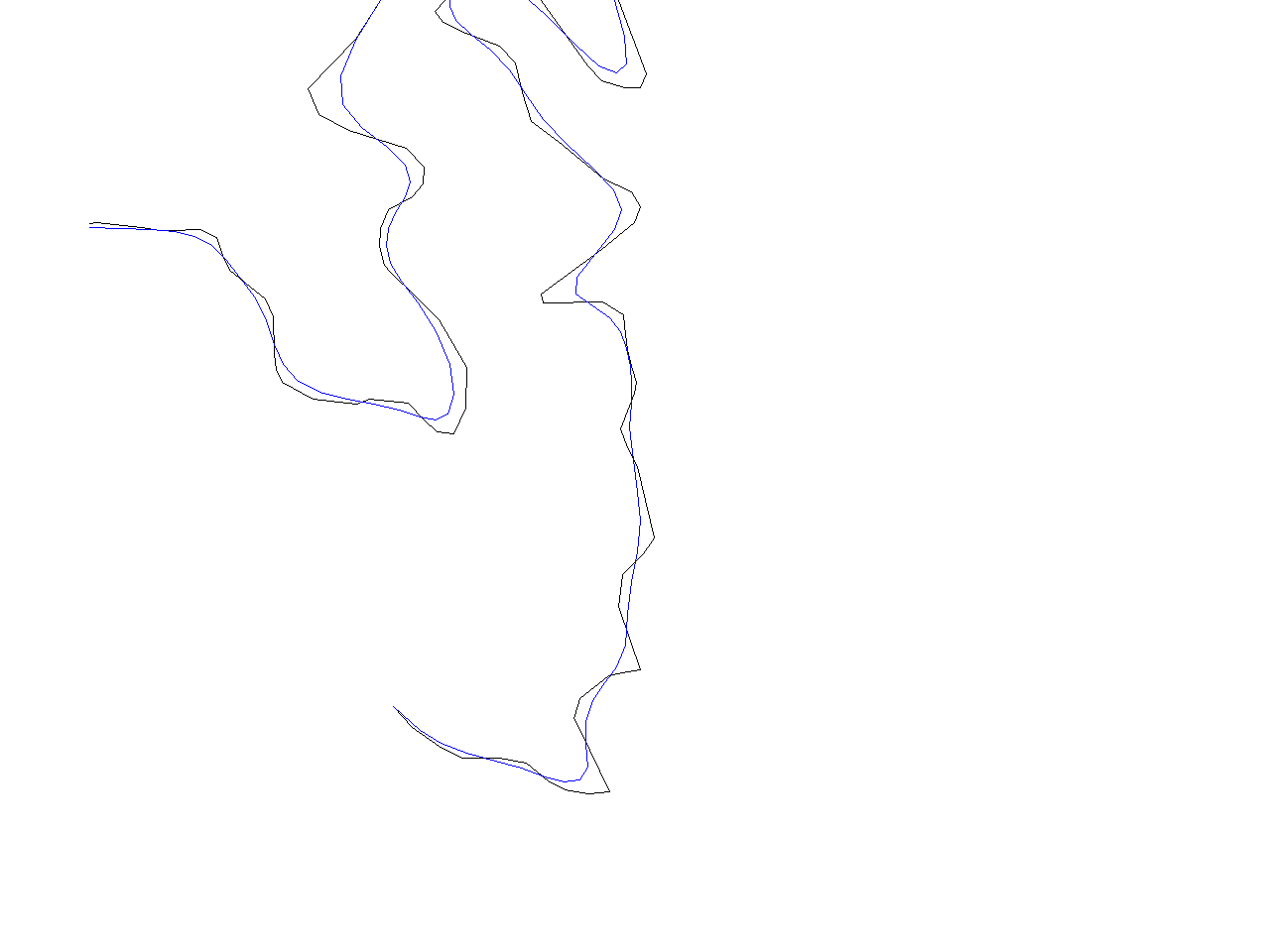
Very similar results can be obtained by Distance Weighting Algorithm (method=distance_weighting). This is not very surprising since these algorithms are almost the same. For example, the image below shows the outputs of "Distance Weighting Algorithm". The image was generated by the following sequence of commands
v.generalize input=roads output=roads_dw1 method=distance_weighting look_ahead=7 slide=1 v.generalize input=roads output=roads_dw2 method=distance_weighting look_ahead=7 slide=0.3 d.erase d.vect roads d.vect roads_dw1 col=red d.vect roads_dw2 col=blue
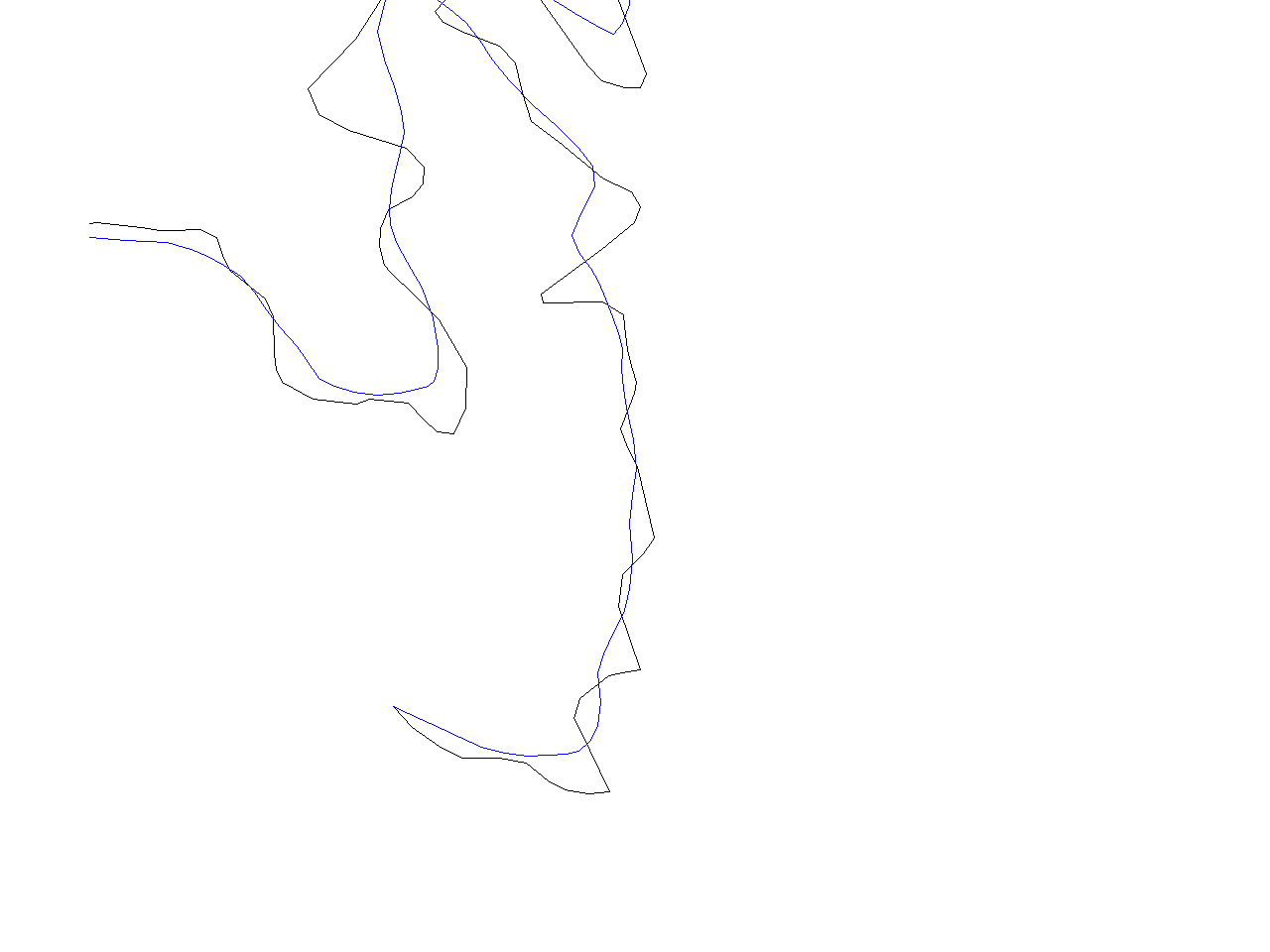
Also, very good resutls can be obtained by the "Snakes" algorithm. On the other hand, it is the (asymptotically) slowest smoothing algorithm implemented in this however. Behaviour of this algorithm is controlled by "alpha" and "beta" parameter. Reasonable range of values for these two parameters is [0..5] where higher values correspond to the straighter lines. Module outputs the input map if alpha=beta=0. And this command
v.generalize input=roads output=roads_snakes method=snakes alpha=1 beta=1
produces a map containing following region (original line is black)
Last smoothing algorithm implemented in this module is "Boyle's Forward-Looking Algorithm" which is another "straightening" algorithm.
v.generalize input=roads output=roads_boyle method=boyle look_ahead=5
produces a map containing following region (original line is black)
Area smoothing example
# spearfish g.region rast=geology r.reclass in=geology out=geology.claysand << EOF 8 = 8 claysand EOF r.to.vect in=geology.claysand out=geology_claysand feature=area v.generalize in=geology_claysand out=geology_claysand_smooth method=snakes
Displacement
If we render entire Spearfish location, we can see in the upper half of the map two interstates which overlap. This is not logically correct (I hope, they do not evarlap in real) and it is also considered as an (presentation) error. For solving such problems, v.generalize provides "dislplacement" method. As the name suggests, this method displaces linear features which are close to each other so that they do not overlap/collide. Method implemented in this modules (based on Snakes) has very good results but not very good perfomance. Therefore the calculations may take few(several) minutes. For this reason, displacement is applied to the simplified lines in this document.
v.generalize input=roads output=roads_dr method=douglas_reduction threshold=0 reduction=50 v.generalize input=roads_dr output=roads_dr_disp method=displacement alpha=0.01 beta=0.01 threshold=100 iterations=35
First command produces simplified lines and then the second command applied displacement operator to the simplified line. Parameters alpha and beta specifies the rigidity of the lines. This means that displacement is bigger for small values of alpha and beta. Also, the displacement is not very significant for higher(>=1.0) values of alpha, beta. Threshold parameter denotes the critical distance. Only the points (and their neighbours) which are closer than threshold apart are displaced by v.generalize. Module tries to move these points such that they are at least threshold apart. However, the displaced points are never threshold (or more) apart for positive values of alpha and beta. Displacement as implemented in v.generalize is an iterative process. Parameter "iterarions" specifies the number of iterations the collisions between the points are resolved. In general, the quality of displacement increases with the number of iterations. However, quality converges quite rapidly and for all maps I tried, the sufficient value of iterations was between 20 and 50. Two command above produce the picture below. Note that it is now possible to distinguish between two "interastate lines" and also observe the free space between interstate and the lines directly below it.
Network Generalization
Network generalization is suitable for selecting "the most important" subnetwork of a network. For example, to select highways, interstates from a road network. Examples in this section work with new GRASS default dataset, which can be downloaded here.
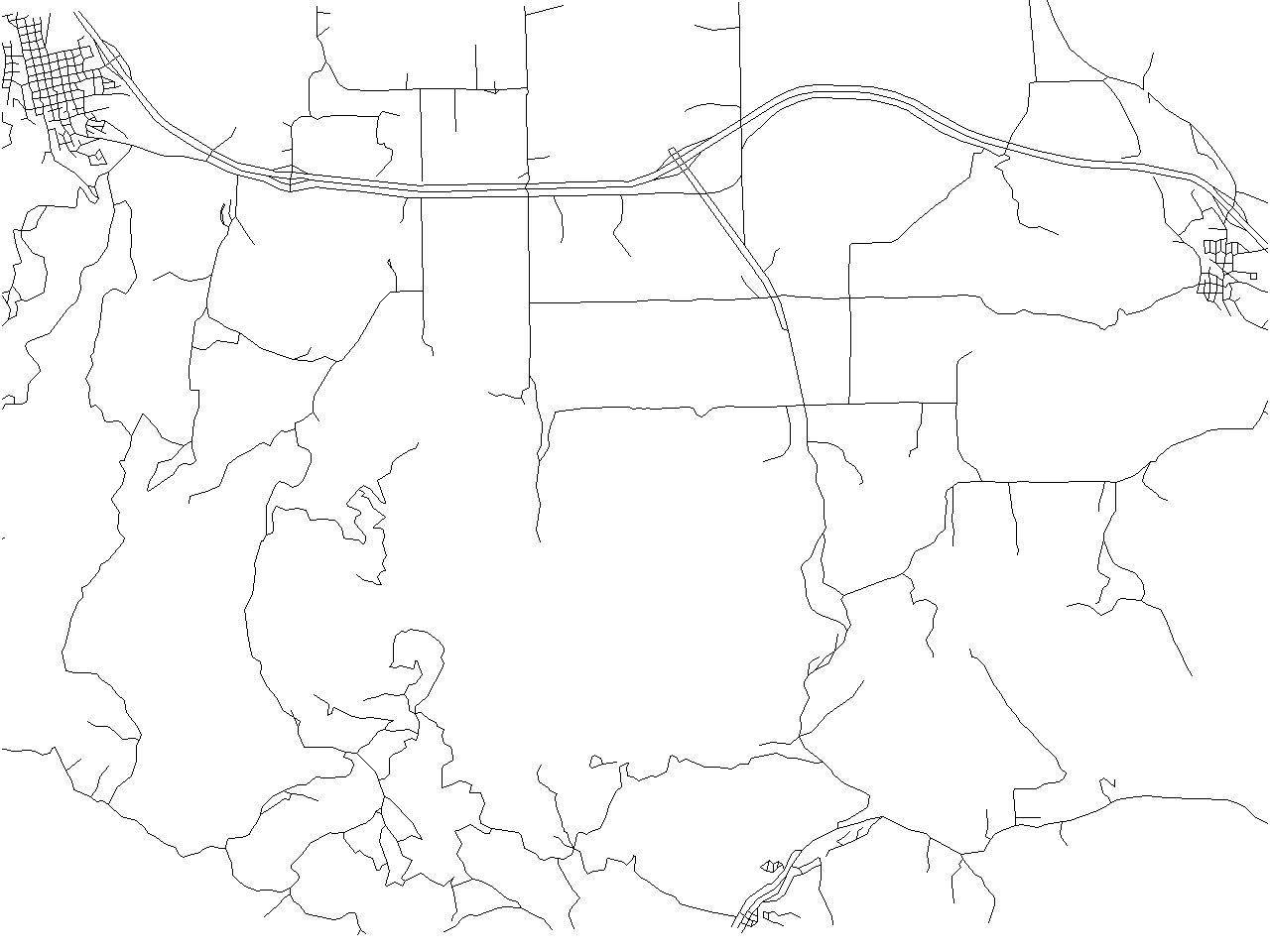
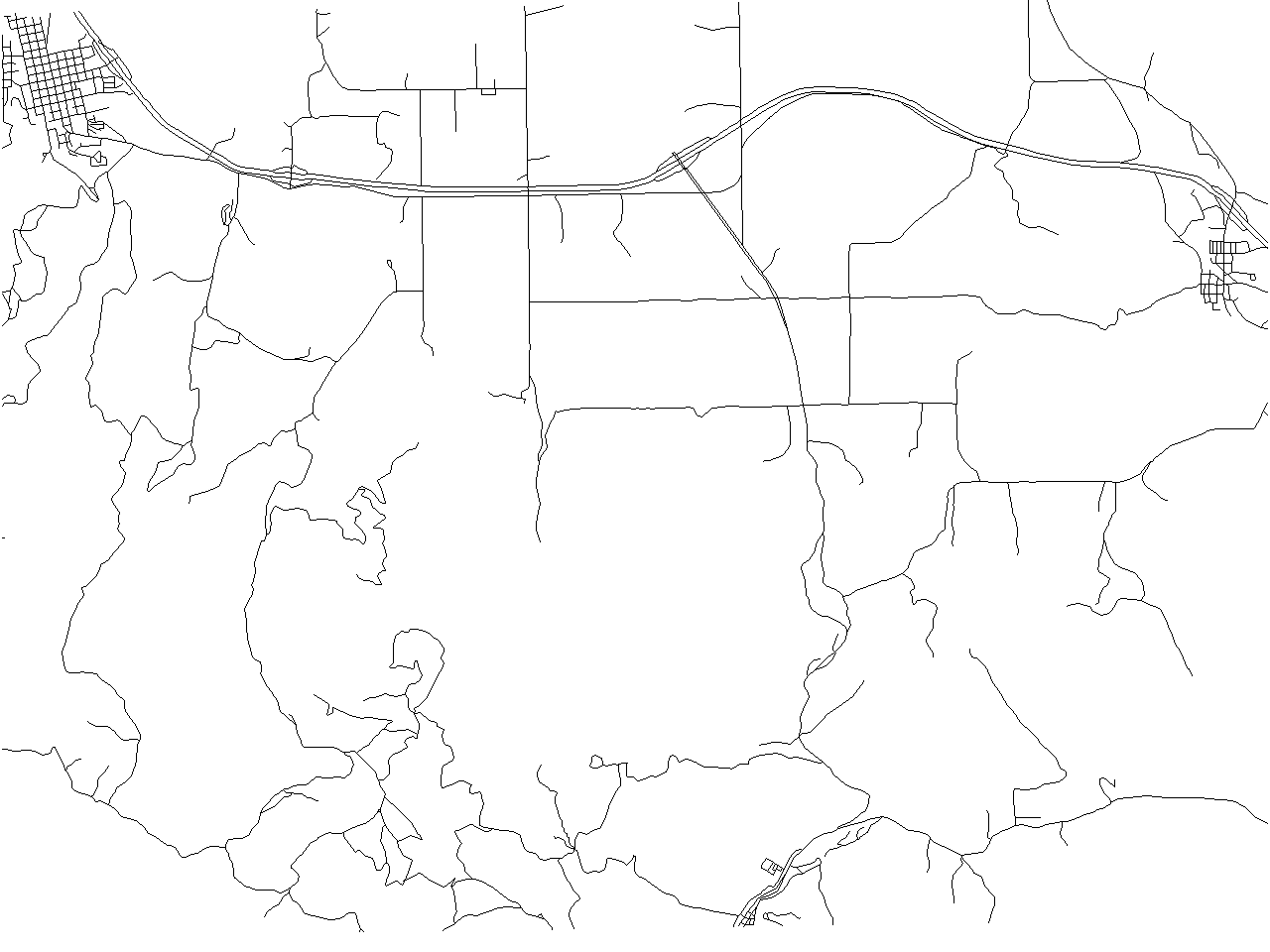
If we render map "streets_wake" we really cannot see the streets, but the only thing we can see is a big black rhombus. We will try to improve this. Firstly, network generalization requites quite a lot of time and memory. Therefore, we begin with simplification of "streets_wake":
v.generalize input=streets_wake output=streets_rs method=remove_small threshold=50
Then we can begin with network generalization. If we execute the folllowing command:
v.generalize input=streets_rs output=streets_rs_network method=network betweeness_thresh=50
we obtain the following map containing "only" 14128. Original map has 49746
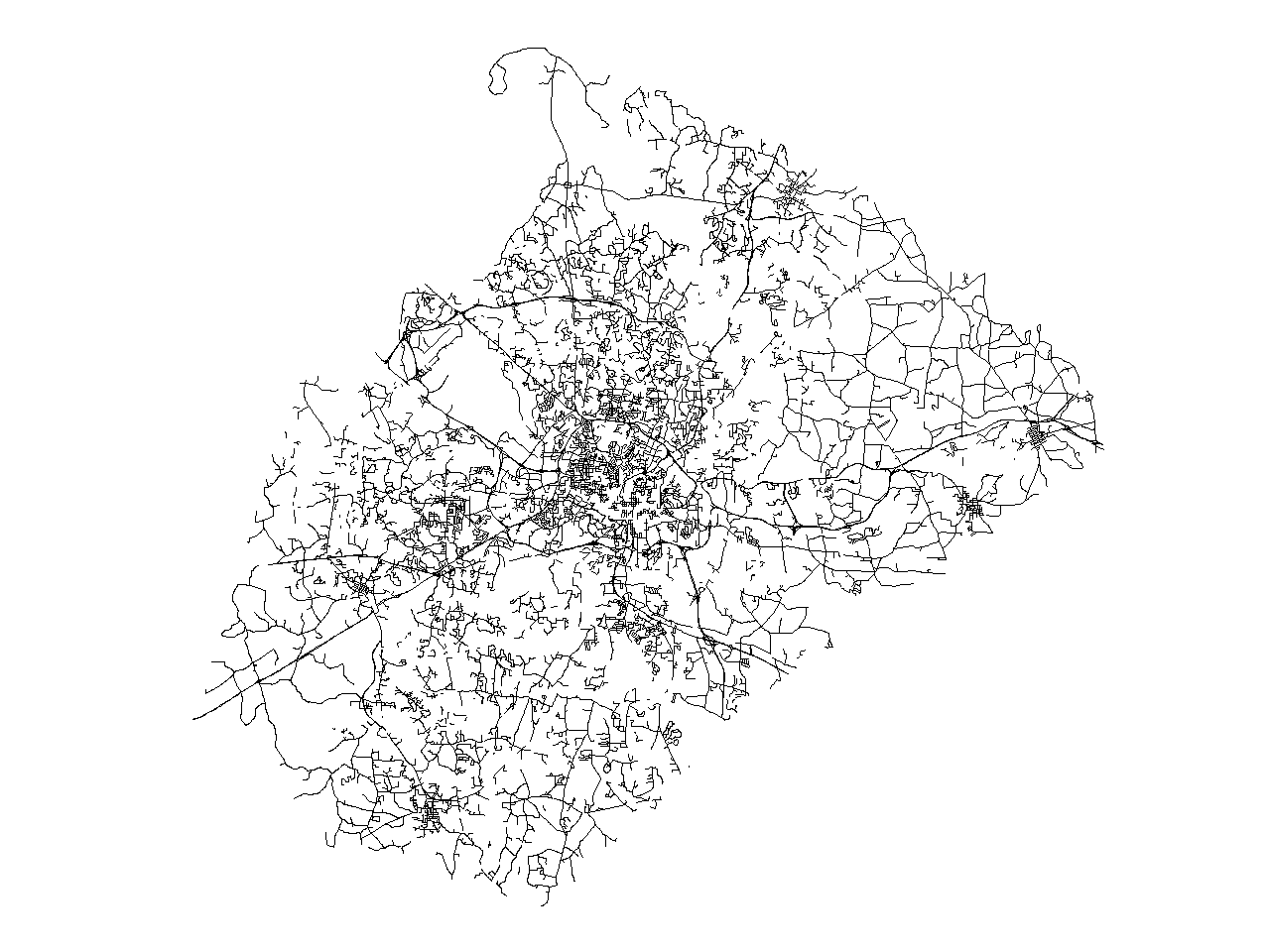
If this is still not enough, we can increase the value of betweeness_thresh to, for example 200. For this value, v.generalize produces following map with 11537 lines.
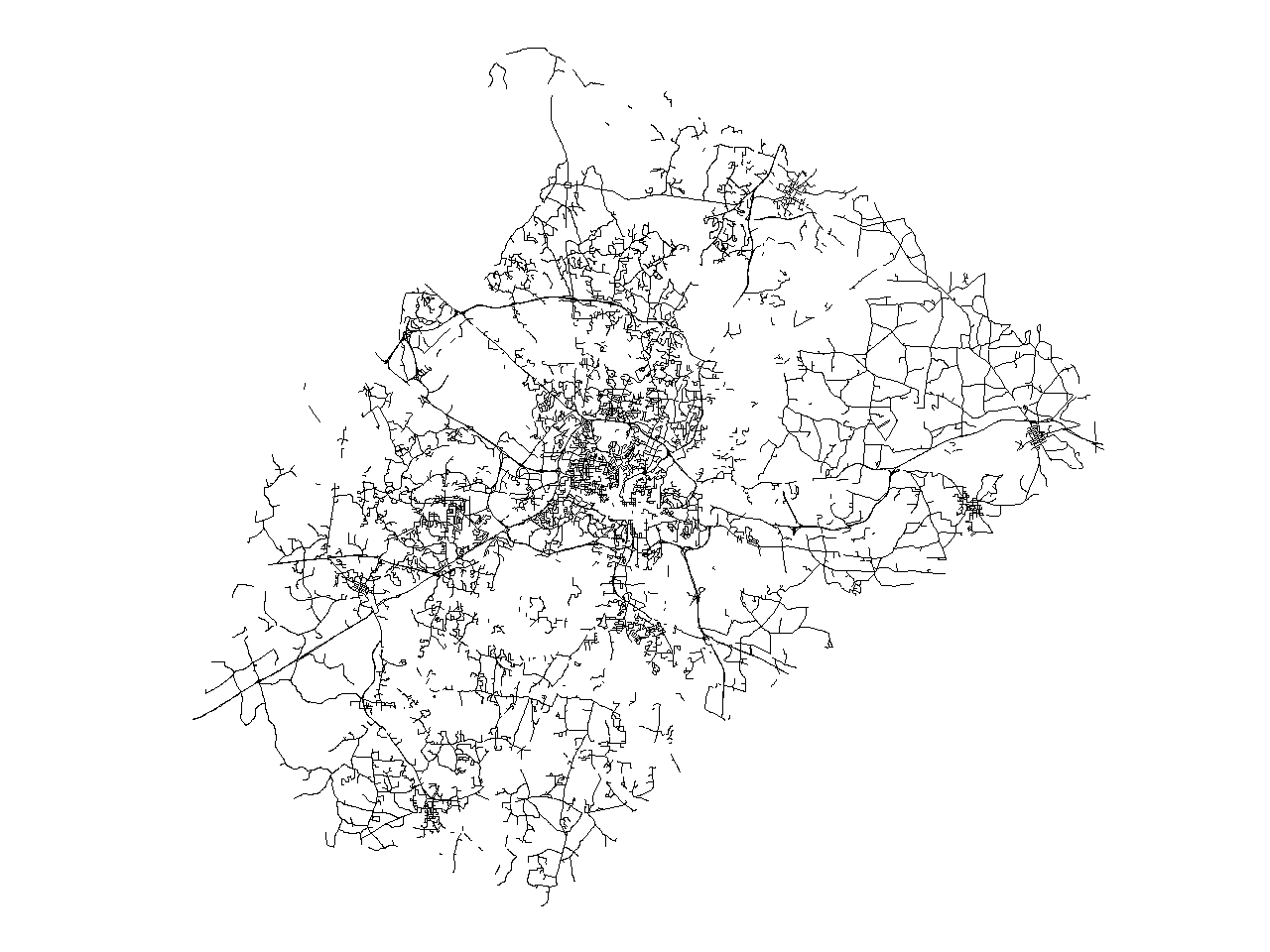
It is also possible to change the values of "closeness_thresh" and "degree_thresh". Parameter "closeness_thresh" is suitable for selecting the "centre(s)" of a network. This parameter is always between 0 and 1. And "reasonable values" of this parameter are smaller for bigger network.
Gereneral Parameters
v.generalize has some parameters and flags which affect the general behaviour of module.
The simplest one is -c flag. "C" stands for copy and if this flag is on then the attributes are copied from the old map to the new map. Note that the attributes of removed features are dropped.
Default behaviour of this module is that the selected algorithm/method is applied to the all lines/areas. It is possible to apply the most of the algorithms only to the selected features. This is achieved by "type", "layer", "cats" and "where" parameters. This works for all algorithms except "Network Generalization" which is always applied to the all features. For example, the following command applies "Douglas Reduction" algorithm to interstates and highways (cat<3) and leaves the other lines unaltered. It also copies the attributes
v.generalize -c input=roads output=roads_douglas_reduction2 method=douglas_reduction threshold=0 reduction=50 type=line layer=1 where="cat<3"
And the following command removes the small areas
v.generalize input=soils output=soils_remove_small method=remove_small threshold=200 type=area
Similarly, the following command displaces only the interstates (cats=1) and the lines with a different category number are not taken into the account.
v.generalize input=roads output=roads_displacement2 method=displacement \ threshold=75 alpha=0.01 beta=0.01 iterations=20 layer=1 cats=1
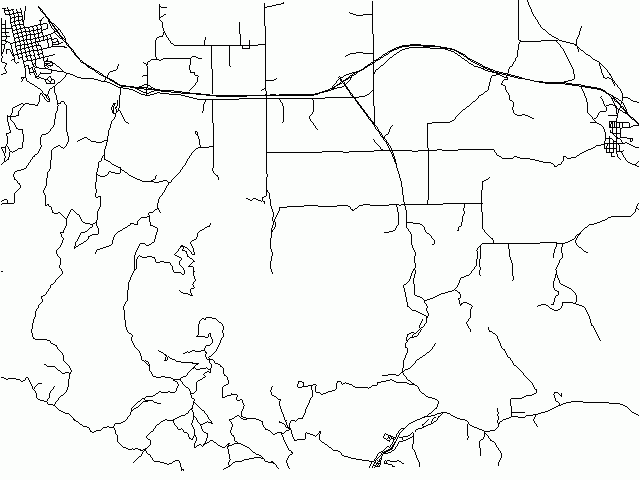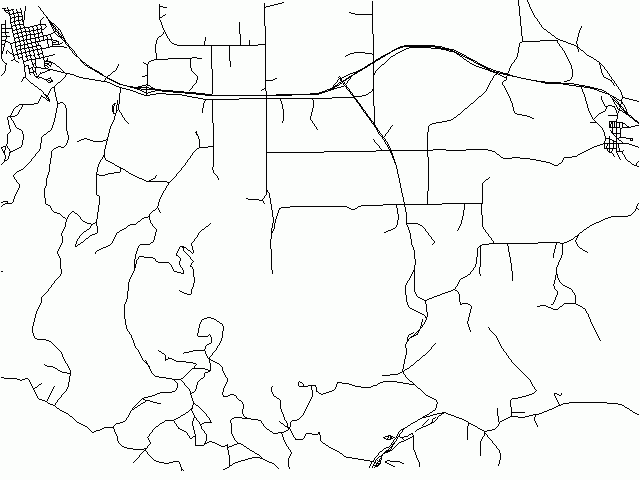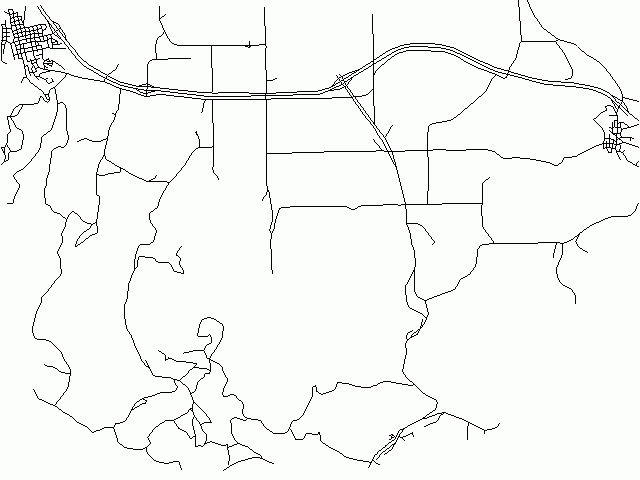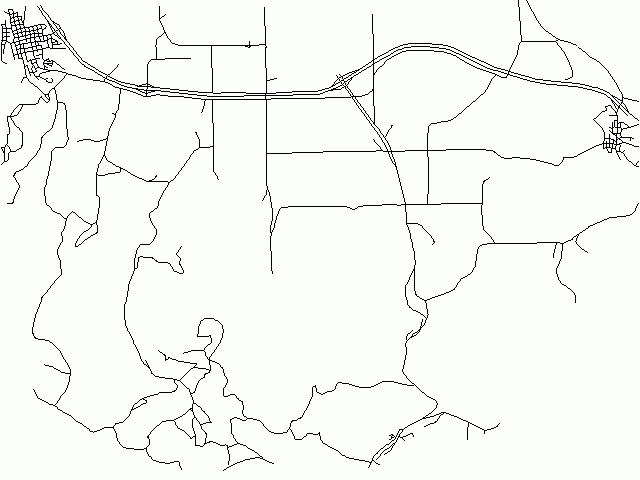
We end up with a complex example of a generalization of "roads" in Spearfish location.
#straighten the lines v.generalize input=roads output=step1 method=snakes alpha=1 beta=1 #simplification v.generalize input=step1 output=step2 method=douglas_reduction threshold=0 reduction=55 #displacement v.generalize input=step2 output=step3 method=displacement alpha=0.01 beta=0.01 threshold=100 iterations=50 #remove small areas v.generalize input=step3 output=step4 method=remove_small threshold=75 #network generalization v.generalize input=step4 output=step5 method=network betweeness_thresh=5 closeness_thresh=0.0425 #smoothing v.generalize input=step5 output=step6 method=chaiken threshold=1 #simplification v.generalize input=step6 output=step7 method=douglas threshold=1 #remove temporary maps g.remove vect=step1,step2,step3,step4,step5,step6
The result "step7" has 655 lines and 3545 vertices and the commands above have the following effect:
References
TODO
See also
Use cases:
AUTHORS
- Daniel Bundala, Google Summer of Code 2007, Student
- Wolf Bergenheim, Mentor
![Reumann-Witkam algorithm result containing 2522 [46%] points](/w/images/V.generalize.reumann.png)
![Douglas algorithm result containing 2107 [38%] points](/w/images/V.generalize.douglas.png)
![Lang algorithm result containing 2160 [39%] points](/w/images/V.generalize.lang.png)
![Vertex Reduction algorithm result containing 4296 [78%] points](/w/images/V.generalize.reduction.png)