SOD Spread tutorial
r.pops.spread is a model for stochastic landscape spread of the pest and pathogens. It uses PoPS (Pest or Pathogen Spread) Core library. In this tutorial we will use it specifically to model the spread of Sudden Oak Death tree disease. This tutorial shows how to run the model. You can download the sample dataset and simulate sudden oak death spread in the Rouge River-Siskiyou National Forest region of western Oregon.
Software
Required software includes:
- GRASS GIS >=7.8
- Addon module:
Input data used in this tutorial
Download the sample dataset containing:
- digital elevation model
- orthophoto of study area
- host layer
- layer of all trees
- roads and rivers
- mapset containing weather coefficients
The sample dataset is a GRASS project, so it goes into your GRASS Database which is usually a directory called grassdata in your home directory or your Documents directory.
Workflow
Download sample data and unzip it into your grassdata. Launch GRASS GIS and select project PoPS_SOD_tutorial and Mapset tutorial.
Change working directory by typing cd (stands for change directory) into the GUI Console and hit Enter. You can create a directory for this exercise (outside of grassdata) anywhere where you can write and read. Navigate to that directory.
Install addon:
g.extension r.pops.spread
First, we will set computational region of our analyses to an extent covering our study area:
g.region region=small_study_area -p
Create files with lists of input maps
Here we used already prepared weather coefficients, these can be created using this workflow. Mapset weather includes raster layers per each week of a simulation. With that, we need to prepare a text file. List and write the maps in a file using g.list:
g.list -m type=raster pattern="average_weather_*" mapset=weather output=weather.txt
The file should be written to your current working directory.
Display infected data
Download color ramp into your current working directory to be used for better visualization of infected cells. Display the infected data. When displaying the infection, do not display zeros.
r.colors map=eu_infection_2019 rules=color_infected.txt
d.rast map=ortho
d.rast map=eu_infection_2019 values=0 -i
d.vect map=NHDFlowline where="FCODE >= 46006" color=30:144:255
d.vect map=roads where="FULLNAME is not NULL" color=165:159:159 width=2
Compute the spread of SOD for default values
Run the model using the text files created and setting only the required parameters. For this analysis we used a wind direction of NE and are looking at the first 5 years of spread from the initial 2019 infection discovery.
We export a result from a single stochastic simulation (with specified random seed).
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 single_series=spread_sod output_frequency=yearly runs=1 random_seed=1
We list newly created output layers representing infected trees in each year of the simulation and we set a custom color ramp.
g.list type=raster pattern="spread_sod*" output=series.txt
r.colors rules=color_infected.txt file=series.txt
You can visualize the spread series in Animation Tool, do not display 0 values for infected maps.
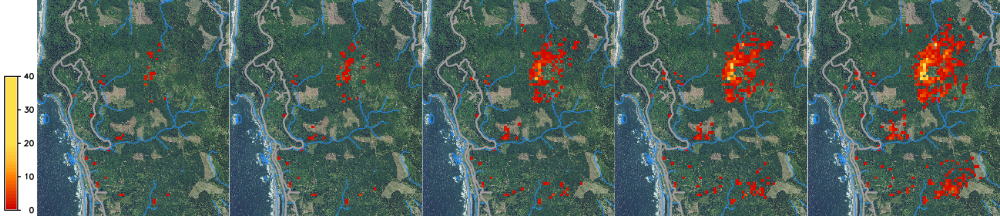
We can run multiple stochastic runs and aggregate the results into a probability layer (0.1 if cell was infected once in 10 runs), average layer (average number of infected trees per cell) and standard deviation layer.
Here we run the process 10x and we use 2 cores for parallel processing (providing module was compiled with OpenMP support and cores are available).
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 average_series=average probability_series=probability stddev_series=stddev output_frequency=yearly runs=10 nprocs=2 random_seed=1
Set color ramp for probability:
g.list type=raster pattern="probability*" output=series.txt --o
r.colors color=magma file=series.txt
Explore results in Map Display or using Animation Tool, omit displaying 0 values of probability.
Effect of dispersal kernel
The choice and parametrization of dispersal kernel significantly influences the spread and should be informed by calibration. The natural dispersal kernel (required) typically represents wind dispersal, additionally, we can optionally add the anthropogenic kernel which represents more human affected spread possibly over longer distances.
Each kernel is defined by type (cauchy, exponential), direction (none, N, NE, E, ...), direction strength (concentration around the direction using von mises distribution) and scale (distance).
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=400 natural_direction_strength=3 single_series=spread_distance output_frequency=yearly runs=1 random_seed=1
g.list type=raster pattern="spread_distance*" output=series.txt --o
r.colors rules=color_infected.txt file=series.txt
Compare our initial run with run with increased kernel scale.
We can then also change the direction to E and increase the strength of direction:
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=E natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=10 single_series=spread_direction output_frequency=yearly runs=1 random_seed=1
g.list type=raster pattern="spread_direction*" output=series.txt --o
r.colors rules=color_infected.txt file=series.txt
Finally, we can select a different kernel type.
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=cauchy natural_distance=242 natural_direction_strength=3 single_series=spread_type output_frequency=yearly runs=1 random_seed=1
g.list type=raster pattern="spread_type*" output=series.txt --o
r.colors rules=color_infected.txt file=series.txt
Effect of reproductive rate
Similarly to kernel, reproductive rate should be informed by calibration. This model uses the Poisson distribution to generate spores. In this example we double it:
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=3 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 single_series=spread_rate output_frequency=yearly runs=1 random_seed=1
g.list type=raster pattern="spread_rate*" output=series.txt --o
r.colors rules=color_infected.txt file=series.txt
Treatments
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=3 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 single_series=spread_rate output_frequency=yearly runs=1 random_seed=1
g.list type=raster pattern="probability*" output=series.txt --o
r.colors color=magma file=series.txt
We treat the initial infection and a buffer around it. The treatments are applied at the end of the year.
r.buffer -z input=eu_infection_2019 output=buffer_A distances=200
r.mapcalc "treatment_A = if (isnull(buffer_A), 0, 1)"
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 probability_series=probtreatmentA output_frequency=yearly runs=10 nprocs=2 random_seed=1 treatments=treatment_A treatment_date=2019-12-31 treatment_length=0 treatment_application=ratio_to_all
g.list type=raster pattern="probtreatmentA*" output=series.txt --o
r.colors color=magma file=series.txt
Here we increase the buffer size:
r.buffer -z input=eu_infection_2019 output=buffer_B distances=500
r.mapcalc "treatment_B = if (isnull(buffer_B), 0, 1)"
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 probability_series=probtreatmentB output_frequency=yearly runs=10 nprocs=2 random_seed=1 treatments=treatment_B treatment_date=2019-12-31 treatment_length=0 treatment_application=ratio_to_all
g.list type=raster pattern="probtreatmentB*" output=series.txt --o
r.colors color=magma file=series.txt
Now we create a large 1km wide barrier in an attempt to stop the spread. For this scenario, we assume the treatment is not 100% effective, but rather only 75% of host is removed.
r.mapcalc "treatment_C = if (y() > 4687000 && y() < 4688000, 0.75, 0 )"
We will see that for the final year of our simulation, the disease spread in several stochastic runs over the barrier:
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 probability_series=probtreatmentC output_frequency=yearly runs=10 nprocs=2 random_seed=1 treatments=treatment_C treatment_date=2019-12-31 treatment_length=0 treatment_application=ratio_to_all
g.list type=raster pattern="probtreatmentC*" output=series.txt --o
r.colors color=magma file=series.txt
Finally, we manage with the 200m buffer treatments A in 2019 and with the barrier in 2021:
r.pops.spread host=host total_plants=max_host infected=eu_infection_2019 start_date=2019-01-01 end_date=2023-12-31 step_unit=week reproductive_rate=1.6 weather_coefficient_file=weather.txt natural_direction=NE natural_dispersal_kernel=exponential natural_distance=242 natural_direction_strength=3 probability_series=probtreatmentAC output_frequency=yearly runs=10 nprocs=2 random_seed=1 treatments=treatment_A,treatment_C treatment_date=2019-12-31,2021-12-31 treatment_length=0,0 treatment_application=ratio_to_all
g.list type=raster pattern="probtreatmentAC*" output=series.txt --o
r.colors color=magma file=series.txt