Contour lines to DEM: Difference between revisions
m (→r.surf.contour) |
|||
| Line 96: | Line 96: | ||
[[Image:Contour1m_surf_scontr.png|thumb|600px|center|r.surf.contour]] | [[Image:Contour1m_surf_scontr.png|thumb|600px|center|r.surf.contour]] | ||
Some thatching artifacts are visible, but otherwise the module represents the surface well and does a | Some thatching artifacts are visible, but otherwise the module represents the surface well and does a decent job recreating the river valleys. | ||
A little extra work is needed to overcome the integer-only aspect of it, but that only takes a minute with {{cmd|r.mapcalc}} as shown below. | A little extra work is needed to overcome the integer-only aspect of it, but that only takes a minute with {{cmd|r.mapcalc}} as shown below. | ||
Revision as of 19:30, 27 February 2010
About

This page will demonstrate and compare a number of different methods of converting vector contour lines into raster DEM surfaces.
Click on images to make them bigger. You may want to download them all at full resolution and then play them back in a quick slide show to highlight the differences. (Images were created in NVIZ at 7x vertical exaggeration)
We will use the North Carolina sample dataset's elev_lid792_cont1m 1m contour line map as the starting point.
First we set the computational region to match the contour lines vector map, and then we force the resolution to align with a 1m grid:
g.region vect=elev_lid792_cont1m g.region res=1 -ap
We can display it on a Xmonitor to be sure:
d.mon x0 d.vect elev_lid792_cont1m -z zcolor=haxby
A number of the r.surf.* modules want the input data to be in raster form already, so we rasterize the contour lines, using the level column for the height values. Also some of the older r.surf.* modules only like to work on integers, so to preserve sub-meter fidelity we do a little trick where we multiply by a large number, do the process, then divide by that number again.
v.to.rast in=elev_lid792_cont1m out=elev.1mcont \ type=line column=level r.mapcalc "elev.1mcont.100k = elev.1mcont * 100000"
r.surf.idw
r.surf.idw (and r.surf.idw2) perform inverse distance weighting interpolation, using the n-closest data points to calculate the elevation of a cell, with the closest points having the greatest weight. As we have already converted to raster in the above v.to.rast step, the data points are evenly spaced in our 1m grid. As we expand the number of search points so that it reaches the next contour line, the lines begin to blur together.
r.surf.idw is much faster but does not create floating-point maps directly. Otherwise the module output is practically identical.
  |
  |
 |
As you can see, r.surf.idw creates a rather terraced DEM so won't be too useful for contour line → DEM tasks. On the other hand, if you look at the central valley it does preserve the overland path of the stream quite well.
Commands used:
NPOINTS=36
r.mapcalc "elev.1mcont.100k = elev.1mcont * 100000"
r.surf.idw in=elev.1mcont.100k out=elev.1mcont.idw.100k npoints=$NPOINTS
r.mapcalc "elev.1mcont.idw_$NPOINTS = elev.1mcont.idw.100k / 100000.0"
g.remove elev.1mcont.idw.100k
r.colors elev.1mcont.idw_$NPOINTS color=haxby
r.surf.nnbathy
The next method we will look at is the r.surf.nnbathy add-on module. It performs a Natural Neighbor interpolation. (see also v.voronoi and v.delaunay)



The two NN interpolations do a reasonable job, with a very nice curved surface in the interpolated areas but contour line artifacts are still clearly visible. If you look closely at the peaks and basins you will notice the minor tension/curvature difference between the two. You can get an idea from this of the very nice DEMs you can create given a good spread of input points to work with instead of contour lines.
The linear TIN operation is very fast, but otherwise creates a low quality DEM compared to the other methods which are able to fill the voids between know data points with curves instead of a flat surface.
If you examine the main valley up the center of the image you will notice all 3 methods have nasty step artifacts along the path of the stream.
Commands used:
for ALG in nn ns l ; do
r.surf.nnbathy in=elev.1mcont out=elev.1mcont.NNsurf.$ALG alg=$ALG
r.colors elev.1mcont.NNsurf.$ALG col=haxby
done
Unfortunately nnbathy relies on the Triangle library, which is only licensed for non-commercial use. Otherwise it would be added as a core module in the main GRASS distribution.
v.surf.rst
v.surf.rst employs an advanced regularized spline with tension interpolation method. It does not guarantee that the surface will touch all input points exactly, but it minimizes the differences over all points on the map. Think about it like a rubber sheet stretched over the input points with a dial to control how stiff or flexible the sheet will be. There are many tuning options available. See the RST Spline Surfaces wiki page for more information.
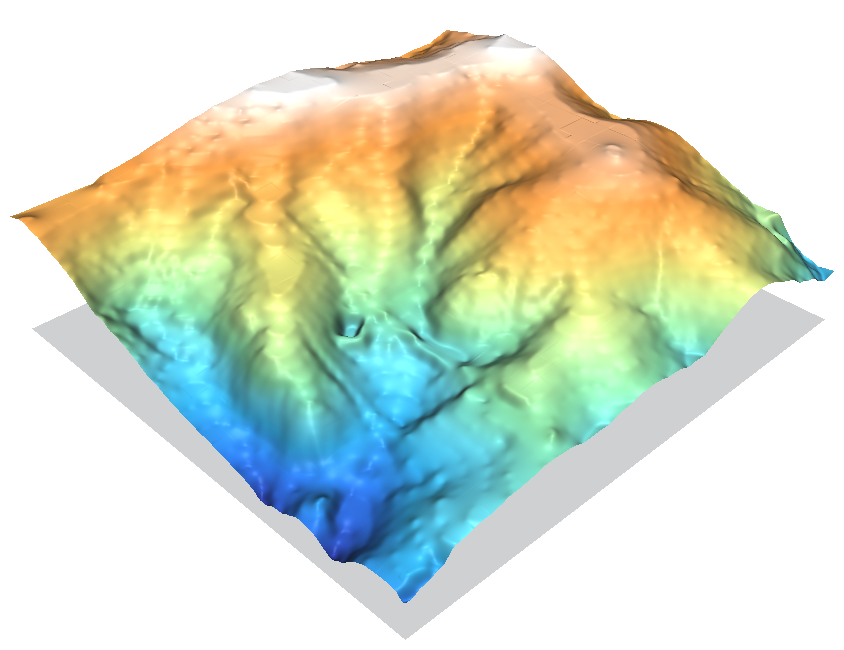
It creates a smooth surface and moulds the shape of the central valley reasonably well.
The RST method does not do well in areas of rapid topographic change (like the base of a cliff), it tends to overshoot requiring the tension parameter to be adjusted; and rapid changes in input point density can lead to quadtree segmentation artifacts (e.g. examine the tops of the hills where there is a large area of no input data). But otherwise it tends to match the shape of the hills quite nicely.
Command used:
v.surf.rst in=elev_lid792_cont1m elev=elev.1mcont.rst zcol=level
r.surf.contour
GRASS's r.surf.contour module is specifically built for converting contour lines into DEMs, and in general it does a rather nice job at it.
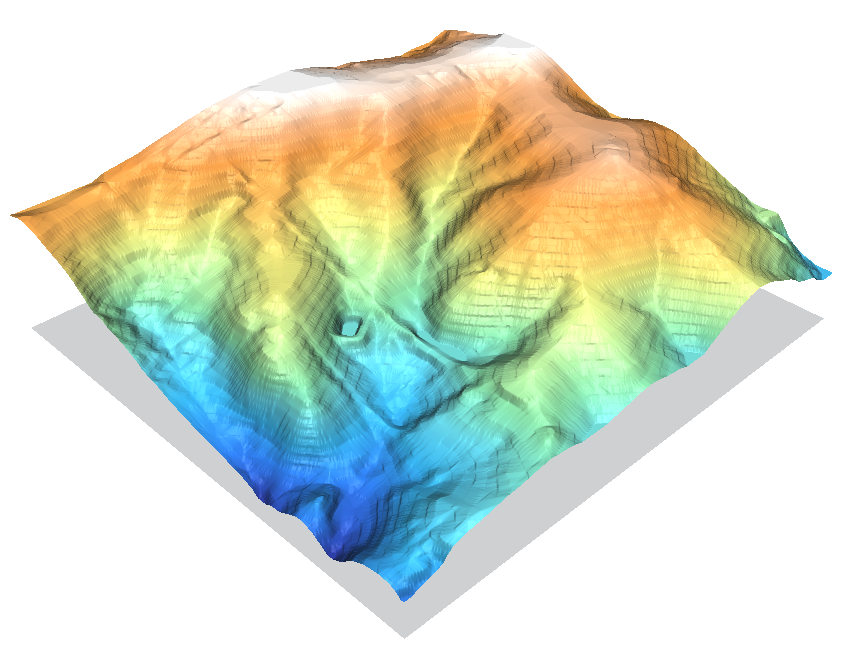
Some thatching artifacts are visible, but otherwise the module represents the surface well and does a decent job recreating the river valleys.
A little extra work is needed to overcome the integer-only aspect of it, but that only takes a minute with r.mapcalc as shown below.
Commands used:
r.mapcalc "elev.1mcont.100k = elev.1mcont * 100000"
r.surf.contour in=elev.1mcont.100k out=elev.1mcont.surf.100k
r.mapcalc "elev.1mcont.surfcont = elev.1mcont.surf.100k / 100000.0"
g.remove elev.1mcont.surf.100k
r.colors elev.1mcont.surfcont col=haxby
Reference images
As a comparison, the following three images show DEMs created by a high-resolution LIDAR survey dataset.
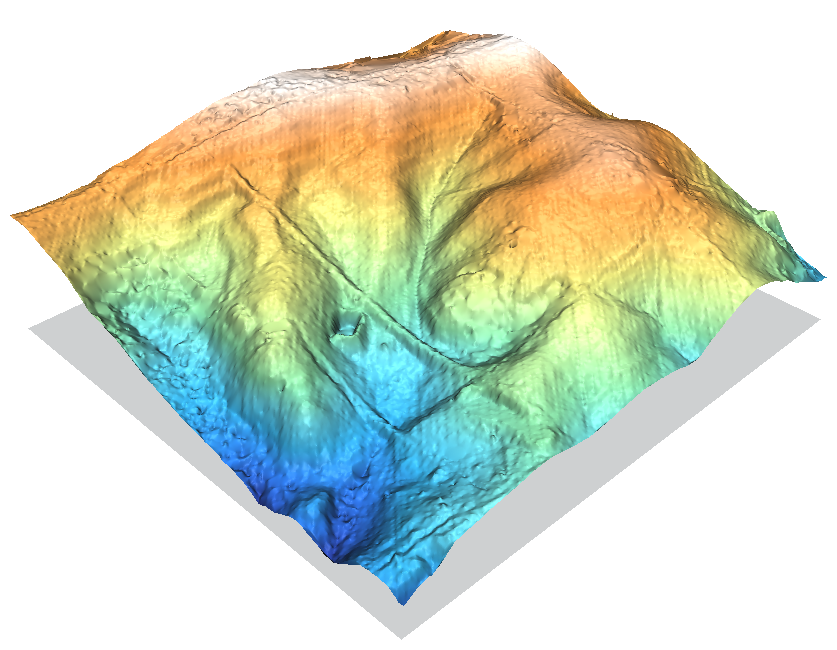
In the above image to preserve consistency with the other DEMs on this page the raster resolution was set finer than the LIDAR data points, so r.in.xyz's nice statistical aggregation filtering is mostly bypassed. With a slightly coarser resolution the scan line artifacts would disappear. r.univar can be used to check the point cloud density with a n count map from r.in.xyz.
Commands used:
v.out.ascii elev_lid792_bepts | \
r.in.xyz in=- x=1 y=2 z=3 out=elev_lid792_bepts.n method=n zrange=102,133
v.out.ascii elev_lid792_bepts | \
r.in.xyz in=- x=1 y=2 z=3 out=elev_lid792_bepts.mean method=mean zrange=102,133
# check
## r.null elev_lid792_bepts.n setnull=0
r.univar elev_lid792_bepts.n
d.histogram elev_lid792_bepts.mean
# nn surfce
r.surf.nnbathy_17 in=elev_lid792_bepts.mean out=elev_lid792_bepts.nn alg=nn
r.colors elev_lid792_bepts.nn col=haxby
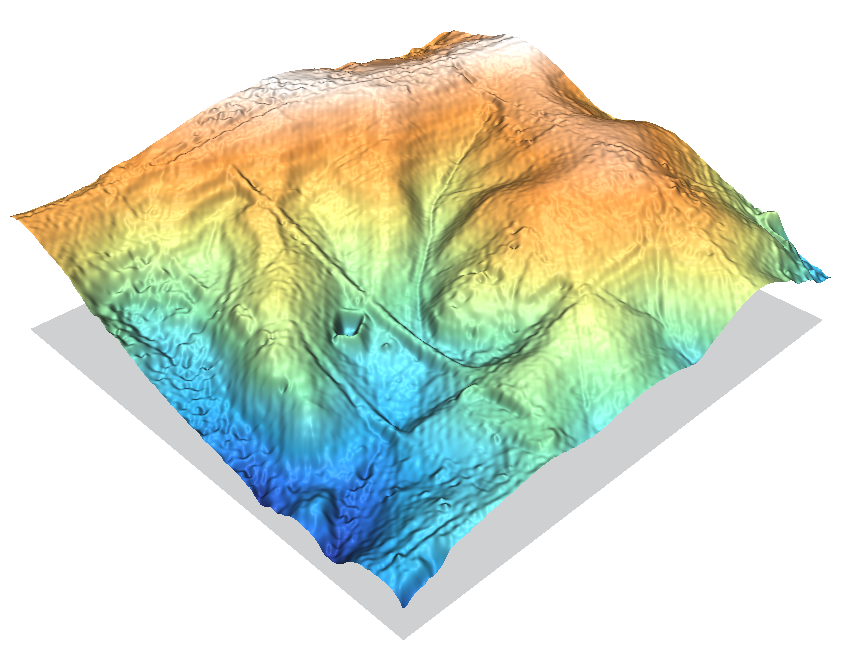
The smoother surface of a regularized spline approach.
Command used:
v.surf.rst in=elev_lid792_bepts elev=elev_lid792_bepts.rst -z layer=0
If should be noted that the LIDAR dataset shown here has been cleaned to provide the true-ground surface. The other LIDAR dataset in the sample dataset (elev_lidrural_mrpts) shows the first-hits, and so the trees in maps created from it would be represented at their full height. Here they look at little shrunken.
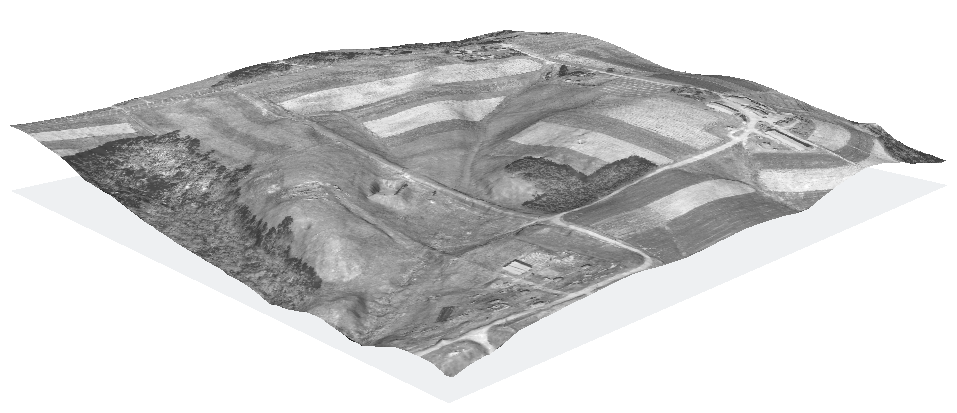
Commands used:
nviz elev=elev_lid792_bepts.nn color=ortho_2001_t792_1m
# export as PPM image from NVIZ, convert to PNG:
for file in *.ppm ; do
pnmtopng $file > `basename $file .ppm`.png
done
# crop away whitespace:
for file in *.png ; do
pngtopnm $file | pnmcrop | \
pnmpad -white -left 10 -right 10 -top 30 -bottom 10 | \
pnmtopng -compression 9 > `basename $file .png`_crop.png
done
Further investigation
You are encouraged to use the r.slope.aspect and r.param.scale modules to further check for artifacts.
For example:
r.slope.aspect elev=elev.1mcont.rst slope=elev.1mcont.rst.slope \ pcurv=elev.1mcont.rst.pcurv tcurv=elev.1mcont.rst.tcurv